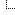The probabilities of winning are around 67% if you switch and 33% if you don't.
First of all, the following facts are critical to a correct understanding of the problem, and need to be stated more explicitly:
1. The host is not malicious. He doesn't just offer a chance to switch when the contestant's original guess is correct. Rather, he always offers the chance. (With a malicious host, it would always be better to stick to your original guess, since the very fact the host gave you a chance to change your mind would mean that your guess was correct!)
2. The host knows where the £10,000 is. When he opens a door to reveal £100, that wasn't an accident; he's never going to open the door that reveals the biggie!
One way to look at the problem is this. If you adopt the non-switching strategy, you will win whenever your original guess was correct (which has a 1/3 probability of happening), and lose otherwise. If you adopt the switching strategy, you will lose whenever your original guess was correct, but you will win whenever your original guess was wrong (which has a 2/3 probability of happening).
This is a good argument in favour of the 1/3, 2/3 theory, but it doesn't explain what's wrong with the 1/2, 1/2 theory. After all, it seems perfectly reasonable that, if a door is opened revealing £100, there should now be a 50-50 chance of the £10,000 being behind one of the remaining two doors.
The key is this. That 1/2, 1/2 theory would be correct if the host opened a door completely at random, and it happened to reveal £100. But (from item 2 above) we know that the host will never open the door revealing £10,000. So there is additional information revealed by the host's choice of which door to open, besides the obvious information that that door revealed £100.
Suppose you choose door 1 and the host opens door 2 (meaning the £10,000 is either behind door 1 or door 3). Although it's true that the basic probabilities of the £10,000 car being behind door 1 or door 3 are equal, that's not the relevant issue here. Instead, we are after the conditional probabilities that £10,000 is behind door 1 or door 3, given that the host opened door 2.
What this means is: think of playing the game many, many times. Obviously, on average the big prize will be behind door 1, 1/3 of these times, behind door 2 1/3 of these times, and behind door 3 1/3 of these times. So, out of all the times you play the game, the proportion that have £10,000 behind door 1 is equal to the proportion that have £10,000 behind door 3.
But the question for us is: if we restrict our attention only to those cases in which you chose door 1 and the host opened door 2, what proportion of those games have £10,000 behind door 1, and what proportion have £10,000 behind door 3? The answers are now no longer equal.
First, think intuitively. On average, for every 6 times you play the game and choose door 1, there will be 2 times when £10,000 is behind door 1 (in which case the host might open either door 2 or door 3, so that means 1 time out of the 6 the host will open door 2, and 1 time out of the 6 the host will open door 3). Also, on average, there will be 2 times when £10,000 is behind door 2 (in which case the host must open door 3), and there will be 2 times when £10,000 is behind door 3 (in which case the host must open door 2).
So on average, for every six times you play the game and choose door 1, there will be
· one time when £10,000 is behind door 1 and the host opens door 2
· one time when £10,000 is behind door 1 and the host opens door 3
· two times when £10,000 is behind door 2 and the host opens door 3
· two times when £10,000 is behind door 3 and the host opens door
Out of all the three times when the host opens door 2, one of them has £10,000 behind door 1 and two of them have it behind door 3. So, out of all the times when you choose door 1 and the host opens door 2, on average 1/3 of those times have £10,000 behind door 1 and 2/3 of those times have 310,000 behind door 3. That's why switching gives you a 2/3 chance of winning.
The way this is formalized mathematically is as follows. Suppose door 1 is your choice. Let A be the event that £10,000 is behind door 1, and B the event that the host opened door 2. What we want is the conditional probability of A, given B. This is the probability of (A and B) divided by the probability of B.
The probability of A is one third (£10,000 has a 1/3 chance of being behind door 1). The probability of (A and B) is one-half the probability of A (since when £10,000 is behind door 1 the host might open either door 2 or door 3, with equal probability). So the probability of (A and B) is 1/6.
The probability of B is one half.
Therefore, the conditional probability of A given B is (1/6)/(1/2) = 1/3.
Similarly, if C is the event that £10,000 is behind door 3, the probability of C is one third, and the probability of (C and B) is also one-third (since when £10,000 is behind door 3 the host has no choice but to open door 2).
Therefore, the conditional probability of C given B is (1/3)/(1/2) = 2/3.
That's a mathematical justification of the fact that switching gives you a 2/3 chance of winning, while sticking with your original choice gives you only a 1/3 chance.
Notice what would be different if the host did not know where £10,000 was and simply opened a door that just happened to reveal £100. In that case, one should ask for the probability that £10,000 is behind door 1 given that the host opened door 2 and given that the door the host opened revealed £100. If you work out that probability, it turns out to be 1/2.
....I really should get out more.